How to
-
A note in abacus
There are several types of abacuses (or abaci) used throughout history and across different cultures. The most popular ones are from China, but there are other abacus that were developed independently. This article gives glimpse of some of the popular abacus. Types of abacus 1. Chinese Abacus (Suanpan) The Suanpan typically has 2 beads on…
-
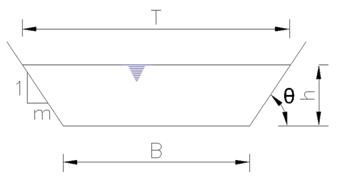
Most efficient trapezoidal section for flow propagation
Calculating the most efficient trapezoidal section of a canal is crucial for optimizing water flow and minimizing the construction cost. A trapezoidal canal section, characterized by its trapezoidal shape, allows for controlled flow and effective sediment transport. The most efficient trapezoidal section of canal can be calculated as follows Let, Base width of the canal=B…
-
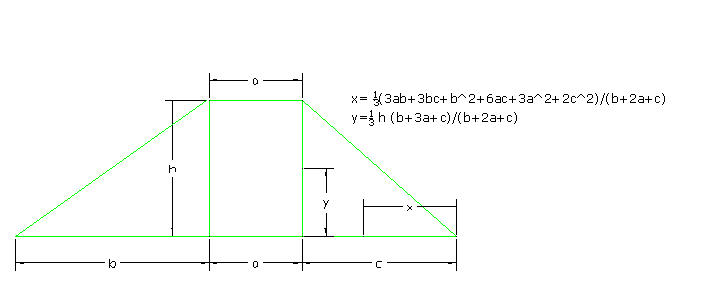
Centroid of trapezoidal shape
The centroid of the trapezoidal with its one face perpendicular is given be $$ X=-1/3* {(-2b^2-2*a*b+a^2)/(a+b)}$$ $$Y=1/3 *h* (b+2*a)/(a+b)$$ Where a, b, h and origin is as shown in the figure below. Similarly, the centroid of any trapezoidal that does not have perpendicular face is given by $$x= 1/3*(3a*b+3*b*c+b^2+6*a*c+3*a^2+2*c^2)/(b+2a+c)$$ $$y=1/3* h* (b+3*a+c)/(b+2*a+c)$$ Where a, b…
-
Common problems in Autocad and their solution – a historical database
I am listing a set of AutoCAD commands and system variable which just offends the regular users. Use F1 in the AutoCAD for details. Problem: Land Desktop import slope lines in plan view Solution: To import end lines (lines meeting to ground in fill or cut): Cross section->Point Output->Catch Pt to DWG-> Yes ->…
-
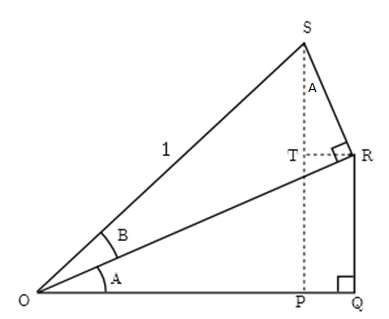
Derivation for sum of angles
The summation formulas for sine, cosine, and tangent are the key identities that govern trigonometric relationships. These formulas help us analyse combinations of angles in various scenarios, from simple geometric calculations to complex oscillatory systems. Let’s revise these fundamental concepts. Derivation Cos(A+B)=OP/OS=(OQ-PQ)/OS =OQ/OS-PQ/OS =OQ/OR*OR/OS-PQ/SR*SR/OS =CosA*CosB-SinA*SinB …………(since PQ=TR) Sin(A+B)=SP/OS=(ST+TP)/OS =ST/OS+TP/OS =ST/SR*SR/OS+TP/OR*OR/OS =CosA*SinB +SinA*CosB ………..(since TP=RQ) Tan(A+B)=Sin(A+B)/Cos(A+B)…
-
Counting the number of words in MS-Word using Fields
Counting the number of words in MS Word document can often feel like a straightforward task—until you need to exclude certain sections like titles, references, or footnotes. Whether you’re preparing a manuscript, a report, or an academic paper, accurately tracking the word count can make a significant difference. Here’s a handy guide to help you…
-
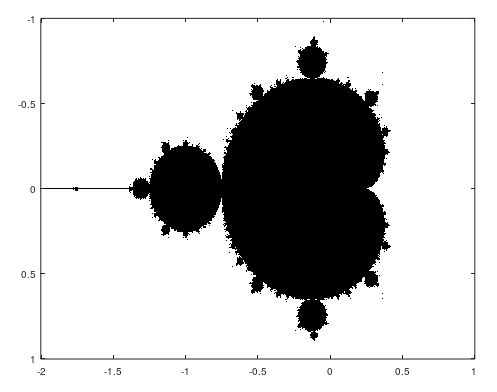
Fractals programming
Fractals are intricate geometric patterns that exhibit self-similarity across various scales. They are created by repeating a simple process, leading to complex structures often found in nature, such as snowflakes, coastlines, and tree branches. The concept of fractals challenges traditional notions of geometry, as they possess non-integer dimensions, meaning their detail increases infinitely with magnification.…
-
Traditional units of land measurement
Land measurement is a crucial aspect of agricultural practices and cultural heritage across the globe. Traditional units of land measurement vary by region, reflecting local customs, agricultural needs, and historical contexts. These units are not merely numerical values; they embody the relationship between people and the land they cultivate. China In China, the mu is…
-
Multiple linear regression analysis with constraints
Multiple linear regression is a statistical technique used to model the relationship between a dependent variable and two or more independent variables. It extends simple linear regression by allowing multiple factors to influence the outcome, making it useful for predicting or understanding the effect of several variables simultaneously. The model takes the form \[ y…