The derivation of the combined angle is essential for understanding the magnitude and direction of forces resulting from bends in both the XY and XZ planes, such as in pipeline design.
Derivation
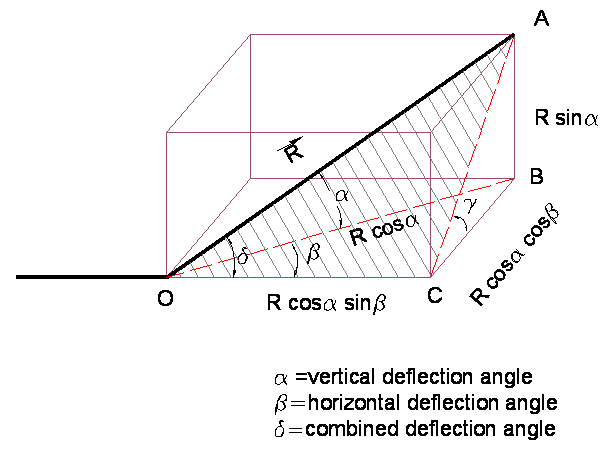
Consider a straight line that deflects at point O along OA, as illustrated in the figure. The angles of deflection are also depicted.
Let R be the position vector of point A. The projection of OA onto the XY plane is denoted as OB, and the projection of OA onto a plane parallel to the YZ plane is AB. Similarly, OC is the projection of line OB along the X-axis, while BC is the projection of OB along the Y-axis.
From the figure, we can derive the following relationships:
- OB = R * cos(α)
- AB = R * sin(α)
- OC = OB * cos(β) = R * cos(α) * cos(β)
- BC = OB * sin(β) = R * cos(α) * sin(β)
Thus, the position vector OA can be expressed as:
R = |R| * (cos(α) * cos(β) * i + cos(α) * sin(β) * j + sin(α) * k)
The unit vector along R is then:
r = (cos(α) * cos(β) * i + cos(α) * sin(β) * j + sin(α) * k)
Combined Deflection Angle
The combined deflection angle δ can be derived from the equation:
r . i = |r| * |i| * cos(δ)
This simplifies to:
r . i = 1 * 1 * cos(δ)
Thus, we have:
cos(δ) = cos(α) * cos(β)
Consequently, the angle δ can be expressed as:
δ = cos^(-1)(cos(α) * cos(β))
This angle δ lies within the OAC plane, as indicated in the figure.
Force Components
If F represents the magnitude of the force due to the deflection δ (for instance, in a pipeline scenario), the horizontal and vertical components of this force are given by:
- Horizontal component: Fx1 = F * r . i = F * cos(α) * cos(β)
- Another horizontal component: Fx2 = F * r . j = F * cos(α) * sin(β)
- Total horizontal force: Fx = F * cos(α)
- Vertical component: Fy = F * r . j = F * sin(α)
This analysis provides a comprehensive understanding of the forces acting on the structure due to combined deflection angles.