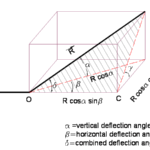
In this post, I will show how to calculate the combined 3d angle. Such situation arises while designing a rigid 3d joints such as a pipeline. The coordinate-based approach can be employed to determine the actual deflection angle between two lines in 3D space. This method not only calculates the deflection angle, but also accurately measures the lengths of the lines involved.
Let us suppose three coordinate points in space and let X be the angle between these two lines
A(x1,y1,z1)
B(x2,y2,z2)
C(x3,y3,z3)
The vector AB is given by,
$$\vec{AB}= (x2-x1)\textbf{i}+(y2-y1)\textbf{j}+(z2-z1)\textbf= a1\textbf{i}+a2\textbf{j}+a3\textbf{k}$$
Similarly, vector BC is given by
$$\vec{AB}= (x3-x2)\textbf{i}+(y3-y2)\textbf{j}+(z3-z2)\textbf{k}=b1\textbf{i}+b2\textbf{j}+b3\textbf{k}$$
The dot product of two vectors is given by,
Equation 1,
$$\vec{AB}.\vec{BC}= AB. BC. cos(x)$$
Here AB and BC=length of segment AB and BC respectively and is given by
$$L1=AB=\sqrt{(a1^2+a2^2+a3^2)}$$
$$L2=BC=\sqrt{(b1^2+b2^2+b3^2)}$$
Substituting in equation 1
$$cosX=\frac{\vec{AB}.\vec{BC}}{L1*L2}$$
Also, the total length will be,
$$L=L1+L2$$
Observe that any two lines joined at a point in space will lie in a single plane.