Finite Element Analysis (FEA) has become a cornerstone in modern engineering, evolving from its humble origins into an advanced computational technique that touches virtually every aspect of structural, mechanical, and material engineering. Its development traces back to the mid-20th century, born out of the need for more accurate solutions to complex engineering problems that could not be solved with classical analytical methods.
Early development
The roots of FEA can be found in the early 1940s when engineers and mathematicians sought ways to improve the structural analysis of aircraft during World War II. The complexity of airplane designs, coupled with the necessity for lighter and more efficient materials, required more sophisticated tools than what was traditionally available. It was in this period that pioneers like Alexander Hrennikoff and Richard Courant made significant strides. In 1941, Hrennikoff used lattice frameworks to analyze elasticity problems, laying the groundwork for future developments. Courant, in 1943, contributed further by employing piecewise polynomial approximations for numerical solutions to partial differential equations.
The real breakthrough came in the 1950s and 60s when engineers such as J. Turner, M.J. Clough, H.C. Martin, and L.J. Topp formalized the finite element method (FEM). Initially, FEA was primarily used in structural engineering for analyzing bridges, buildings, and mechanical parts. Its key innovation was the discretization of continuous structures into smaller, finite elements, each governed by simple equations that, when assembled together, represented the entire system. This allowed engineers to approximate complex geometries and behaviors, a capability that revolutionized structural analysis.
Rise of computational power
The advent of digital computers in the 1960s further accelerated the development of FEA. Engineers could now automate the complex calculations required for large-scale models, which made the method more accessible and practical for real-world engineering challenges. By the 1970s, commercial FEA software emerged, such as NASTRAN, ANSYS, and ABAQUS, which are still widely used today. These tools enabled engineers to simulate stresses, heat transfer, fluid flow, and dynamic responses in a wide range of fields.
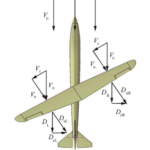
In contemporary engineering, FEA is indispensable, finding applications across various industries, including automotive, aerospace, civil, and bioengineering. In automotive design, FEA helps optimize the strength and safety of vehicles while minimizing weight, improving fuel efficiency. Aerospace engineers rely on FEA to model the structural integrity of aircraft components, subject to high stresses and temperature variations. In civil engineering, it is used to assess the stability of bridges and buildings, particularly in earthquake-prone areas.
Modern FEA extends beyond mechanical and structural systems. In biomedical engineering, for instance, FEA is used to simulate the behavior of biological tissues and medical implants, such as prosthetic limbs and artificial joints. This enables the design of more durable and functional medical devices. It is also used in electronics to model heat dissipation in circuits, ensuring that devices remain operational under high thermal loads.
With advancements in computational power, modern FEA software can handle increasingly complex problems, providing engineers with tools to analyze non-linear materials, large deformations, and multiphysics problems (combining thermal, structural, and fluid dynamics). FEA simulations now complement experimental testing, allowing for rapid prototyping, cost reduction, and improved safety standards.
Conclusion
Finite Element Analysis has evolved from a niche mathematical method into a vital tool for modern engineering. As technology continues to advance, FEA will play an even more critical role in shaping innovations in multiple fields, pushing the boundaries of what engineers can model, simulate, and ultimately create.