Inception
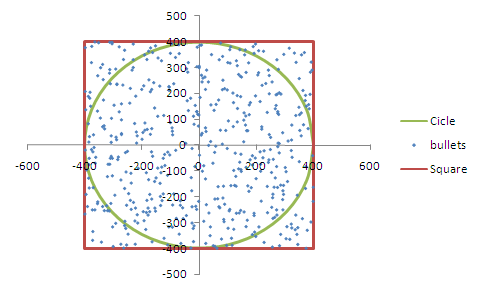
While reading “Fooled by Randomness” by Nassim Nicholas Taleb, I came across a chapter discussing Monte Carlo theory. The author claimed that when bullets are fired inside a square and a circle is inscribed within it, the ratio of bullets inside the circle to the total number of bullets approximates a ratio involving π. This prompted me to investigate the exact value of this ratio, so I created an Excel sheet to explore it.
Methodology
I simulated the process using approximately 17,150 bullets (or points), generated randomly within the boundaries of the square. An inscribed circle was drawn within this square, and I employed the distance formula to determine whether each point lay inside the circle. I then counted the total number of bullets inside the circle and the overall number of bullets, calculating the resulting ratio.
Simulation
I experimented with varying the size of the square and the radius of the circle to observe how the ratio changed. I found that when the circle is perfectly inscribed within the square, the ratio approaches π/4. You can also play with the file attached below.
Attachment:
monte carlo pi sumulation.xlsx