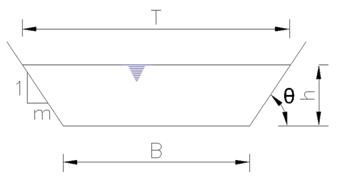
Calculating the most efficient trapezoidal section of a canal is crucial for optimizing water flow and minimizing the construction cost. A trapezoidal canal section, characterized by its trapezoidal shape, allows for controlled flow and effective sediment transport. The most efficient trapezoidal section of canal can be calculated as follows
Let,
Base width of the canal=B
Side slope=m (1V:mH)
Flow depth = h
Wetted perimeter= P
The cross-sectional area,
$$A=B*h+m*h^2 $$
ie $$B= (A-m*h^2)/h $$
ie $$B=A/h-m*h $$
Wetted perimeter
$$P= B+2*h *sqrt(m^2+1) $$
$$ P=A/h-m*h+2*h *sqrt(m^2+1) $$
For most efficient channel,
$$dP/dh=0 $$
ie $$-A/h^2-m+2 sqrt(m^2+1)=0 $$ (area will be constant because it is necessary to carry the required flow)
Substitute value of A
$$-(B*h+m*h^2)/h^2-m+2 sqrt(m^2+1)=0 $$
$$-B/h-m-m+2 sqrt(m^2+1)=0 $$
Therefore,
$$B/h=2*sqrt(m^2+1)-2*m$$
is the required relationship.