The Euler formula, one of the most remarkable equations in mathematics, elegantly connects complex analysis, trigonometry, and exponential functions. It is named after the Swiss mathematician Leonhard Euler, who first introduced it in the 18th century.
The formula is expressed as:
$$e^{ix} = \cos{x} + i\sin{x}$$
Where:
e is the base of the natural logarithm,
i is the imaginary unit (where
cosx and sinx are the trigonometric functions cosine and sine, respectively.
Historical background
Euler first published this relationship in 1748 in his work Introductio in analysin infinitorum, which explored infinite series, functions, and complex numbers. The formula unified previously separate branches of mathematics, linking trigonometric and exponential functions through complex numbers. Euler’s insight built on earlier work involving complex numbers by mathematicians such as René Descartes and Abraham de Moivre. However, it was Euler who discovered the deep connection between exponential functions and trigonometry.
Derivation
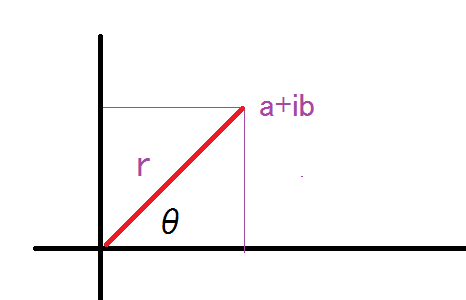
We start in a complex plane. In this place any point can be represetnted by
$$a+ib=r(cosθ+ i sinθ)$$
From Tylor’s series:
$$F(x)=F(0)+x*f’(x)/1!+x^2*f’’(0)/2!+……+x^n*fn(0)/n!+….$$
Therefore,
$$Sin(x)=x-x^3/3!+x^5/5!-x^7/7!+….$$
$$Cos(x)=1-x^2/2!+x^4/4!-x^6/6!+….$$
$$e^{x}=1+x+x^2/2!+x^3/3!+..$$
Now,
$$e^{ix}=1+ix+(ix)^2/2!+(ix)^3/3!+(ix)^4/4!+(ix)^5/5!+…$$
$$e^{ix}=(1-x^2/2!+x^4/4!-x^6/6!+…)+i(x-x^3/3!+x^5/5!-x^7/7!+…)$$
$$=cos(x)+i*sin(x)$$