The summation formulas for sine, cosine, and tangent are the key identities that govern trigonometric relationships. These formulas help us analyze combinations of angles in various scenarios, from simple geometric calculations to complex oscillatory systems. Let’s revise these fundamental concepts.
Derivation
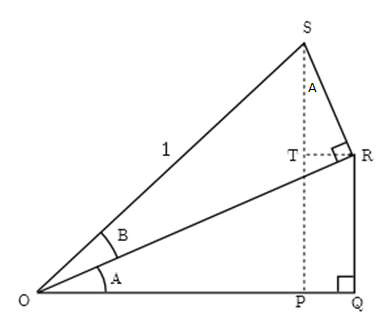
Cos(A+B)=OP/OS=(OQ-PQ)/OS =OQ/OS-PQ/OS =OQ/OR*OR/OS-PQ/SR*SR/OS =CosA*CosB-SinA*SinB …………(since PQ=TR) Sin(A+B)=SP/OS=(ST+TP)/OS =ST/OS+TP/OS =ST/SR*SR/OS+TP/OR*OR/OS =CosA*SinB +SinA*CosB ………..(since TP=RQ) Tan(A+B)=Sin(A+B)/Cos(A+B) =(SinA*CosB+CosA*SinB)/(CosA*CosB-SinA*SinB) =(TanA+TanB)/(1-TanA*TanB)………(dividing both side by CosA*CosB)
For A-B note that sin is an odd function and cos is an even function, therefore, Sin(-A)=-SinA and Cos(-A)=Cos(A). Graphically this means the cos function is symmetric over x axis while sine function is not so.